Search Fracture Mechanics Website

Fracture Mechanics

Prev Up Next
with detailed explanations and examples

Description

Crack

Continuum Mechanics Website

www.continuummechanics.org is my sister website. It covers all the fundamental aspects of mechanics - stress, strain, principal values, Hooke's Law, von Mises Stress, etc - in the presence of finite deformations and rotations.

Thank You

Thank you for visiting this web page. Feel free to email me if you have questions or comments.

Please consider visiting an advertiser here. Doing so helps generate revenue that supports this website and its continued development.

Bob McGinty
bmcginty@gmail.com
This website presents the fundamental principles of fracture mechanics, with many examples included. It covers both linear (LEFM) and nonlinear fracture mechanics, including J-Integrals, as well as fatigue crack growth concepts and mechanisms.

Author   Bob McGinty, PhD, PE(ret)
Email    bmcginty@gmail.com



THIS WEBSITE IS UNDER CONSTRUCTION. I expect it to take several years to complete. In the meantime, I welcome all input, suggestions, and contributions to improve its quality and usefulness.



Table of Contents

  1. INTRODUCTION

    1. Historical Background
    2. Complex Numbers
    3. Airy Stress Functions
    4. Plane Stress and Strain

  2. LINEAR ELASTIC FRACTURE MECHANICS

    1. Stress Concentrations at Holes
    2. Stresses at Elliptical Holes
    3. Griffith's Energy Release Rate
    4. Westergaard's Solution for Cracks
    5. Stress Intensity Factor, K
    6. Crack Tip Displacements
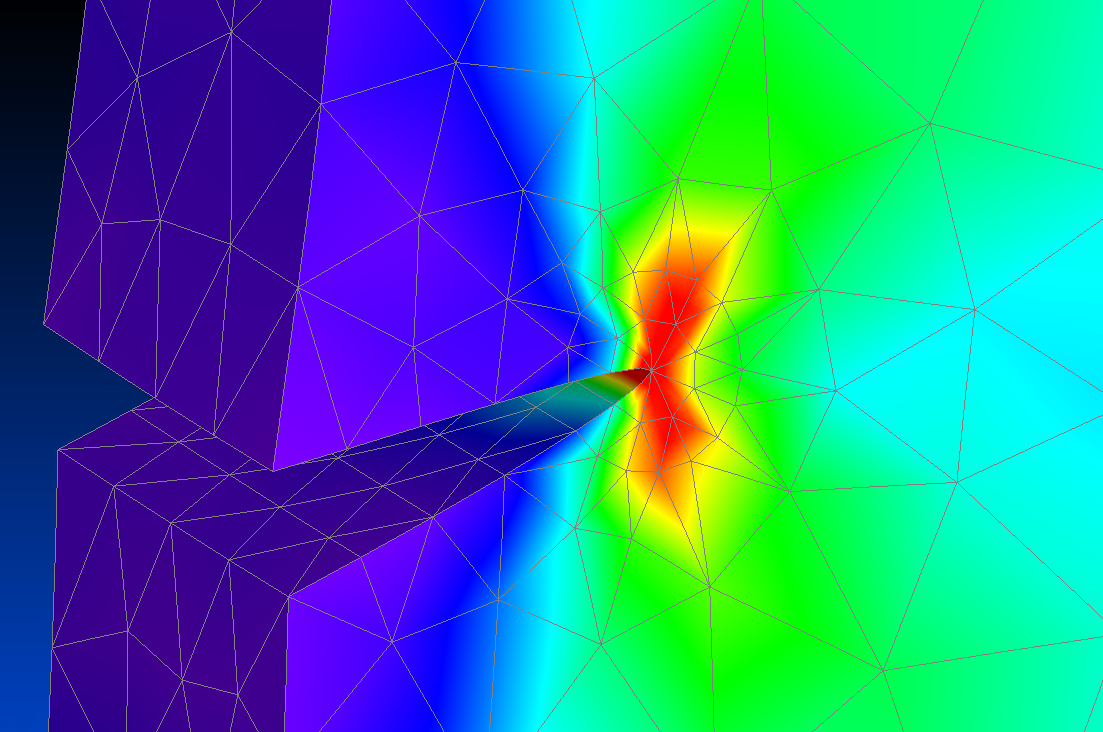
    7. FEA Meshing Guidelines
    8. Determining K from Displacements
    9. Loading Modes I, II, III (in development)

  3. NONLINEAR FRACTURE MECHANICS

    1. The J-Integral
    2. Path Independence of J-Integral

Additional References


Continuum Mechanics Website

Visit my sister website, www.continuummechanics.org, for information on continuum mechanics. It covers all the fundamental aspects of mechanics - stress, strain, principal values, Hooke's Law, von Mises Stress, etc - in the presence of finite deformations and rotations.

A Note About The Web Technologies Used Here

Two relatively new web technologies are used on these pages. The first is Scalable Vector Graphics, or SVG. Pages on this site will display SVG files in compatible browsers, and PNG files in incompatible ones. The advantage of SVG over PNG is that SVG graphics can be scaled to any size without pixelization occurring. SVG files used here were created using Inkscape, an excellent graphics program available free on the internet here.

The second new technology used here is MathJax, a Javascript based display engine for mathematical equations programmed in the LaTeX language. MathJax eliminates the need to display equations as GIF or PNG graphics files (or even SVG for that matter). MathJax requires only the following line of code in the <HEAD> segment of a web page.

<script type="text/javascript" src="https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.5/latest.js?config=TeX-MML-AM_CHTML"></script>

It is then possible to program any math expression in the HTML source using the LaTeX language. For example, typing \(\sigma_{ij}\) produces \( \sigma_{ij} \).

Bob McGinty
October 2014